
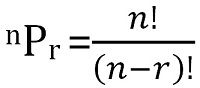
The next lesson will introduce you to combinations or selections. I hope that you now have some idea about circular arrangements. Therefore, the total number of ways in this case will be 2! x 3! or 12. After fixing the position of the women (same as ‘numbering’ the seats), the arrangement on the remaining seats is equivalent to a linear arrangement. This is because after the women are seated, shifting the each of the men by 2 seats will give a different arrangement. Note that we haven’t used the formula for circular arrangements now. Now that we’ve done this, the 3 men can be seated in the remaining seats in 3! or 6 ways. That is why we have only 2 arrangements, as shown in the previous figure. That is, if each woman shifts by a seat in any direction, the seating arrangement remains exactly the same. Note that the following 6 arrangements are equivalent: We’ll first seat the 3 women, on alternate seats, which can be done in (3 – 1)! or 2 ways, as shown below. (We’re ignoring the other 3 seats for now.) For example, using this formula, the number of permutations of five objects taken two at a time is (For k n, nPk n Thus, for 5 objects there are 5 120 arrangements.) For combinations, k objects are selected from a set of n objects to produce subsets without ordering. Solution Since we don’t want the men to be seated together, the only way to do this is to make the men and women sit alternately.

Therefore the required number of ways will be 24 – 12 or 12.Įxample 3 In how many ways can 3 men and 3 women be seated at around table such that no two men sit together? Similar to (i) above, the number of cases in which C and D are seated together, will be 12. The total number of ways will be (5 – 1)! or 24. (ii) The number of ways in this case would be obtained by removing all those cases (from the total possible) in which C and D are together. Therefore, the total number of ways will be 6 x 2 or 12. Let’s take a look at these arrangements:īut in each of these arrangements, A and B can themselves interchange places in 2 ways. This kind of problem refers to a situation where order matters. So, effectively we’ve to arrange 4 people in a circle, the number of ways being (4 – 1)! or 6. 1.Start with an example problem where youll need a number of permutations without repetition. Solution (i) If we wish to seat A and B together in all arrangements, we can consider these two as one unit, along with 3 others. Solution As discussed in the lesson, the number of ways will be (6 – 1)!, or 120.Įxample 2 Find the number of ways in which 5 people A, B, C, D, and E can be seated at a round table, such that Formula The formula for permutation of n objects for r selection of objects is given by: P (n,r) n/ (n-r) For example, the number of ways 3rd and 4th position can be awarded to 10 members is given by: P (10, 2) 10/ (10-2) 10/8 (10.9.8)/8 10 x 9 90 Click here to understand the method of calculation of factorial. Permutations and Combinations A-Level Statistics revision covering permutations. In this lesson, I’ll cover some examples related to circular permutations.Įxample 1 In how many ways can 6 people be seated at a round table?


 0 kommentar(er)
0 kommentar(er)
